|
|
||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
Project Description
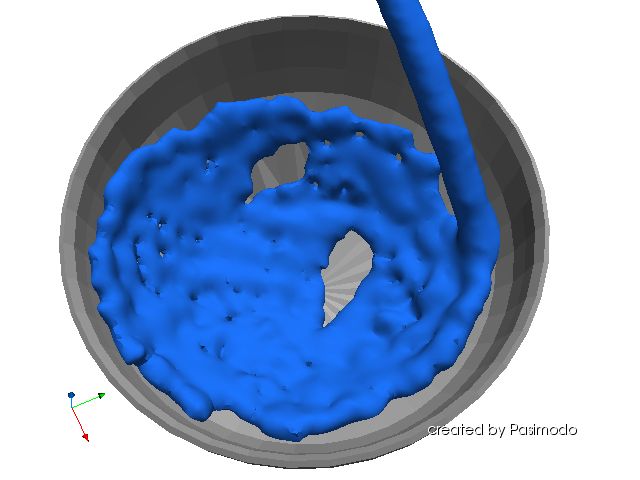
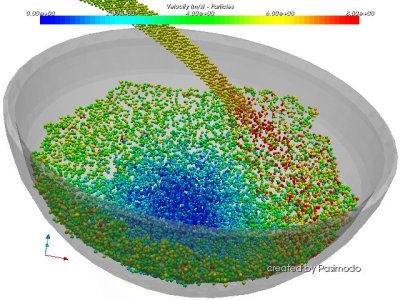
To discretize a partial differential equation using the SPH method, the considered volume is subdivided. These subdivisions are then reduced to one point, the so-called particle, which gets all the important values such as velocity, density but also tension and thermal energy as a mean value taken over the whole subdivision. Therefore, particles are partial volumes with an undefined volume expansion, that move along the velocity field of the represented matter. The spatial functions in the differential equation can now be approximated by smoothing and summing up the discrete values at the particle positions using a kernel function, often similar to a Gaussian function. The approximation's spatial derivatives can be calculated straight away due to the differentiable kernel function. This leaves an ordinary differential equation in time that can be solved with one of the many time stepping schemes. LinksInformation about the particle simulation software Pasimodo, which is applied and enhanced in the framework of this project.To the SPH videos. To the complete Pasimodo Showroom. Contact |
| Last modified
30.9.2015 ( |